피보나치 수
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
피보나치 수는 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, ...과 같이 앞의 두 항을 더하여 다음 항을 만들어 나가는 수열이다. 이 수열은 기원전 5세기에 인도 수학자에 의해 처음 언급되었고, 유럽에서는 레오나르도 피보나치가 토끼의 번식을 연구하면서 널리 알려졌다. 피보나치 수는 황금비와 밀접한 관련이 있으며, 자연 현상, 수학, 금융 등 다양한 분야에서 발견된다. 피보나치 수열의 정의를 변형하여 트리보나치 수, 테트라나치 수와 같은 유사 수열을 만들 수 있으며, 뤼카 수와 같은 다른 수열도 피보나치 수열과 유사한 방식으로 정의된다. 파이썬을 사용하여 재귀, 메모이제이션, 반복 등의 방법으로 피보나치 수를 계산하는 코드를 구현할 수 있다.
더 읽어볼만한 페이지
- 피보나치 수 - 레오나르도 피보나치
레오나르도 피보나치는 힌두-아라비아 숫자 체계를 유럽에 소개하고 피보나치 수열을 제시하여 중세 수학 발전에 기여했으며, 상업 발달을 돕는 《산반서》를 저술하고 황금비와 관련된 피보나치 수열이 다양한 분야에서 활용되도록 했다. - 피보나치 수 - 피보나치 힙
피보나치 힙은 최소 힙 속성을 가진 트리들의 집합으로, 각 노드의 차수를 특정 로그 값 이하로 유지하여 효율적인 삽입, 병합, 최소값 검색 연산을 지원하며, 다익스트라 알고리즘과 같은 그래프 알고리즘의 성능 향상에 활용된다. - 정수열 - 실베스터 수열
실베스터 수열은 각 항이 이전 항들의 곱에 1을 더한 값으로 정의되는 정수 수열로서, 재귀적으로 정의되며 이중 지수 함수적으로 증가하고, 이집트 분수 및 탐욕 알고리즘과 관련이 있으며, 역수 합은 1로 수렴한다. - 정수열 - 소수 (수론)
소수는 1과 자기 자신만을 약수로 가지는 1보다 큰 자연수이며, 무한히 많고 정수론의 기본 정리에서 중요한 역할을 하며 다양한 분야에 응용된다.
| 피보나치 수 |
|---|
2. 역사
피보나치 수가 처음 언급된 문헌은 기원전 5세기 인도의 수학자 핑갈라가 쓴 책이다.
유럽에서는 레오나르도 피보나치가 1202년 출판한 『산반서』(Liber Abaci)에서 토끼의 번식 문제를 통해 이 수열을 소개하면서 널리 알려졌다. 피보나치는 다음과 같은 가상 상황을 설정했다:[3]
- 한 쌍의 토끼는 태어난 지 2개월 후부터 매달 한 쌍의 토끼를 낳는다.
- 토끼는 죽지 않는다.
- 이 조건 하에서, 새로 태어난 한 쌍의 토끼는 1년 동안 총 몇 쌍으로 늘어날까?
이 문제의 조건에 따르면, 토끼 쌍의 수는 다음과 같이 증가한다. 첫 달에는 새로 태어난 한 쌍만 존재한다. 두 번째 달에도 번식할 수 없으므로 그대로 한 쌍이다. 세 번째 달에는 첫 달의 토끼 쌍이 번식하여 새로운 한 쌍을 낳으므로 총 두 쌍이 된다. 네 번째 달에는 세 번째 달에 있던 두 쌍 중 원래 있던 한 쌍만 번식 가능하므로 새로운 한 쌍이 태어나 총 세 쌍이 된다. 다섯 번째 달에는 네 번째 달에 있던 세 쌍 중 두 쌍(두 달 이상 된 토끼)이 번식하여 새로운 두 쌍을 낳으므로 총 다섯 쌍이 된다. 이처럼 특정 달의 토끼 쌍의 수는 바로 전 달과 그 전전 달의 토끼 쌍의 수를 합한 것과 같아지는데, 이는 피보나치 수열의 정의와 일치한다.
매달 토끼 쌍의 수는 다음 표와 같이 변하며, 피보나치 수가 나타나는 것을 확인할 수 있다.
| 갓 태어난 쌍 | 생후 1개월의 쌍 | 생후 2개월 이후의 쌍 | 쌍의 수(합계) | |
|---|---|---|---|---|
| 0개월 후 | 1 | 0 | 0 | 1 |
| 1개월 후 | 0 | 1 | 0 | 1 |
| 2개월 후 | 1 | 0 | 1 | 2 |
| 3개월 후 | 1 | 1 | 1 | 3 |
| 4개월 후 | 2 | 1 | 2 | 5 |
| 5개월 후 | 3 | 2 | 3 | 8 |
| 6개월 후 | 5 | 3 | 5 | 13 |
| 7개월 후 | 8 | 5 | 8 | 21 |
| 8개월 후 | 13 | 8 | 13 | 34 |
| 9개월 후 | 21 | 13 | 21 | 55 |
| 10개월 후 | 34 | 21 | 34 | 89 |
| 11개월 후 | 55 | 34 | 55 | 144 |
| 12개월 후 | 89 | 55 | 89 | 233 |
'''피보나치 수''' 는 0번째 항을 0, 1번째 항을 1로 두고, 2번째 항부터는 바로 앞의 두 항의 합으로 정의되는 수열이다. 즉, 다음과 같은 점화식으로 정의된다.
피보나치 수라는 명칭은 레오나르도 피보나치의 저서에서 비롯되었지만, 그보다 앞서 인도의 학자 헤마찬드라(Hemachandra)가 운율 연구 과정에서 이 수열을 발견하여 기록했다는 사실도 알려져 있다.[1][2]
3. 정의
:
:
:
(때로는 로 정의하기도 한다.)
피보나치 수의 처음 몇 항은 다음과 같다.
:0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, ...
이 수열은 1202년 레오나르도 피보나치(Leonardo Fibonacci)가 저술한 『산반서』(Liber Abaci)에 소개되면서 '피보나치 수'라는 이름으로 널리 알려졌다. 하지만 그보다 앞서 인도의 학자 헤마찬드라(Hemachandra)가 운율 연구 과정에서 이 수열을 발견하여 기록한 바 있다.[1][2]
레오나르도 피보나치는 『산반서』에서 다음과 같은 문제를 통해 이 수열을 설명했다.[3]
시간에 따른 토끼 쌍의 수는 다음 표와 같이 증가하며, 매달 총 토끼 쌍의 수가 바로 피보나치 수가 됨을 알 수 있다.
| 갓 태어난 쌍 | 생후 1개월의 쌍 | 생후 2개월 이후의 쌍 | 쌍의 수(합계) | |
|---|---|---|---|---|
| 0개월 후 | 1 | 0 | 0 | 1 |
| 1개월 후 | 0 | 1 | 0 | 1 |
| 2개월 후 | 1 | 0 | 1 | 2 |
| 3개월 후 | 1 | 1 | 1 | 3 |
| 4개월 후 | 2 | 1 | 2 | 5 |
| 5개월 후 | 3 | 2 | 3 | 8 |
| 6개월 후 | 5 | 3 | 5 | 13 |
| 7개월 후 | 8 | 5 | 8 | 21 |
| 8개월 후 | 13 | 8 | 13 | 34 |
| 9개월 후 | 21 | 13 | 21 | 55 |
| 10개월 후 | 34 | 21 | 34 | 89 |
| 11개월 후 | 55 | 34 | 55 | 144 |
| 12개월 후 | 89 | 55 | 89 | 233 |
3. 1. 일반항
피보나치 수의 일반항은 다음과 같다.[20]:
여기서 는 황금비이며, 이다. 또한 는 5의 음이 아닌 제곱근이다.
이 식은 '''비네 공식'''(Binet's formula영어)이라고 불린다. 이 공식은 1730년 아브라함 드 무아브르가 처음 발견했고, 1765년 레온하르트 오일러가 발표했으나 잊혔다가, 1843년 자크 비네에 의해 다시 발표되었다.[3] 비네가 최초 발견자는 아니다.
황금비 는 이차 방정식 의 두 해 중 큰 값이다. 다른 해를 라고 하면, 일반항은 다음과 같이 나타낼 수도 있다.
:
이므로, 이 커짐에 따라 항은 0에 가까워진다. 따라서 이 충분히 크면 피보나치 수 은 에 매우 가까워진다. 즉, 다음 근사식이 성립한다.
:
실제로 에 대해
4. 성질
피보나치 수는 여러 흥미로운 항등식을 만족한다. 대표적인 것으로 '''카시니 항등식'''(Cassini's identity영어)이 있다.
:
또한, '''도가뉴 항등식'''(d'Ocagne's identity영어)도 성립한다.[20]
:
황금비
:
피보나치 수는 점화식을 이용해 음의 정수 항으로 확장할 수 있다. 이 경우, 다음과 같은 관계가 성립한다.[20]
: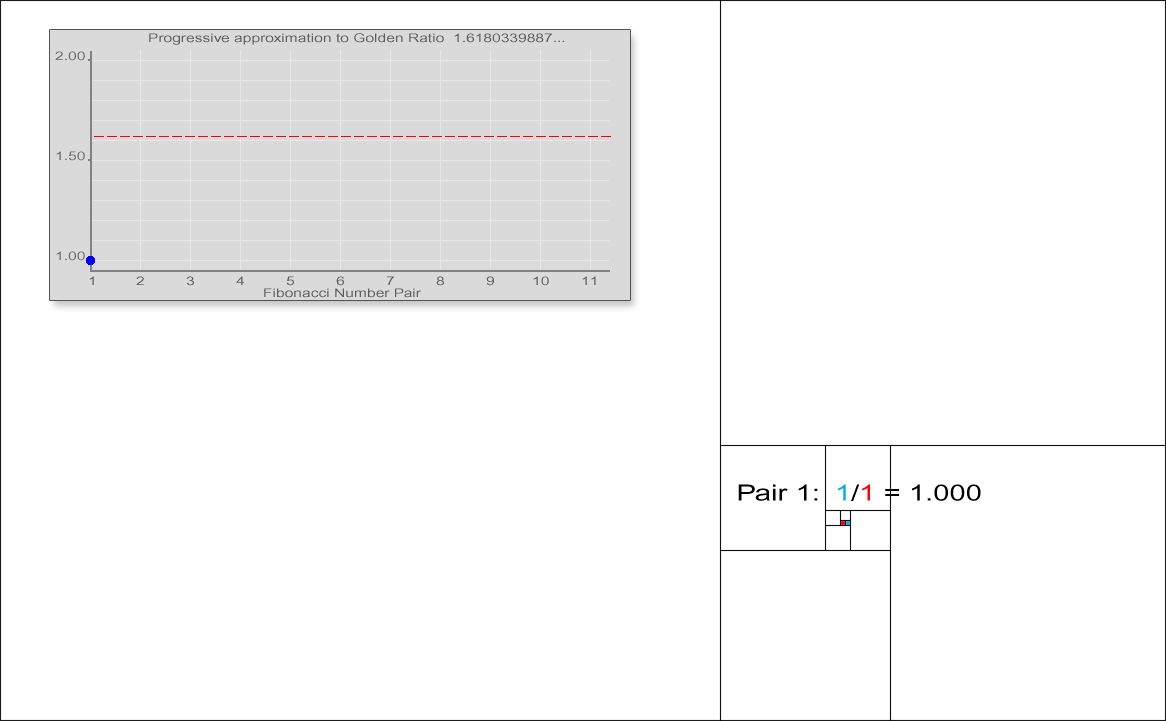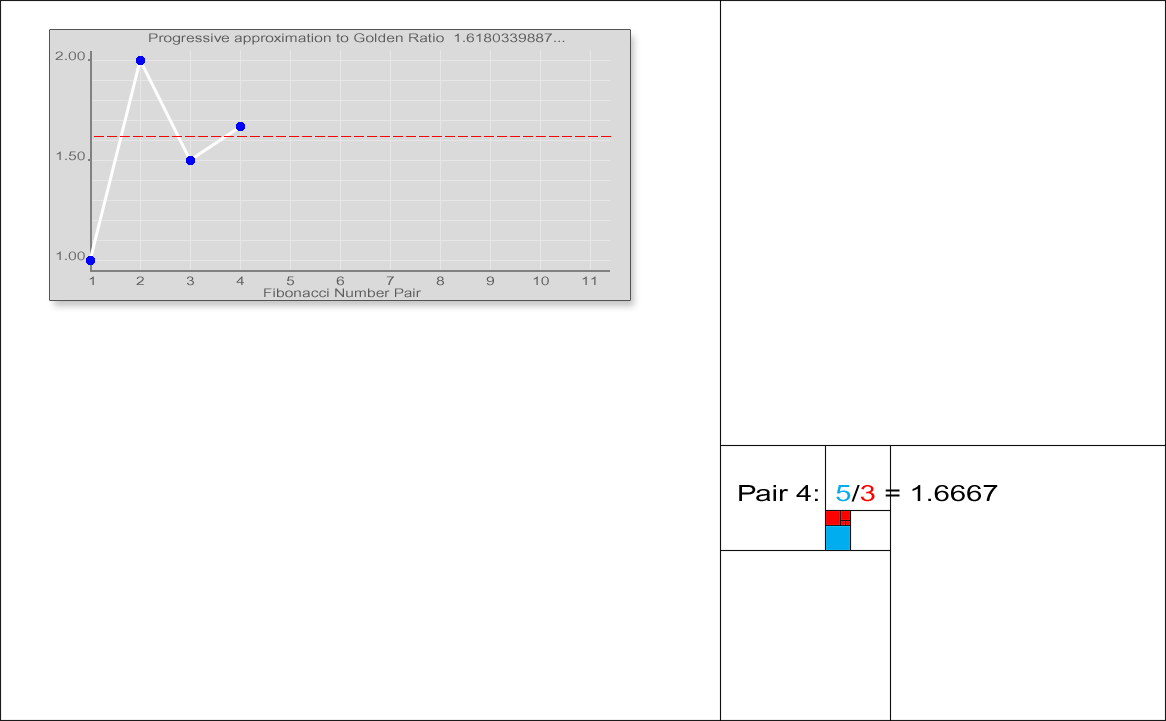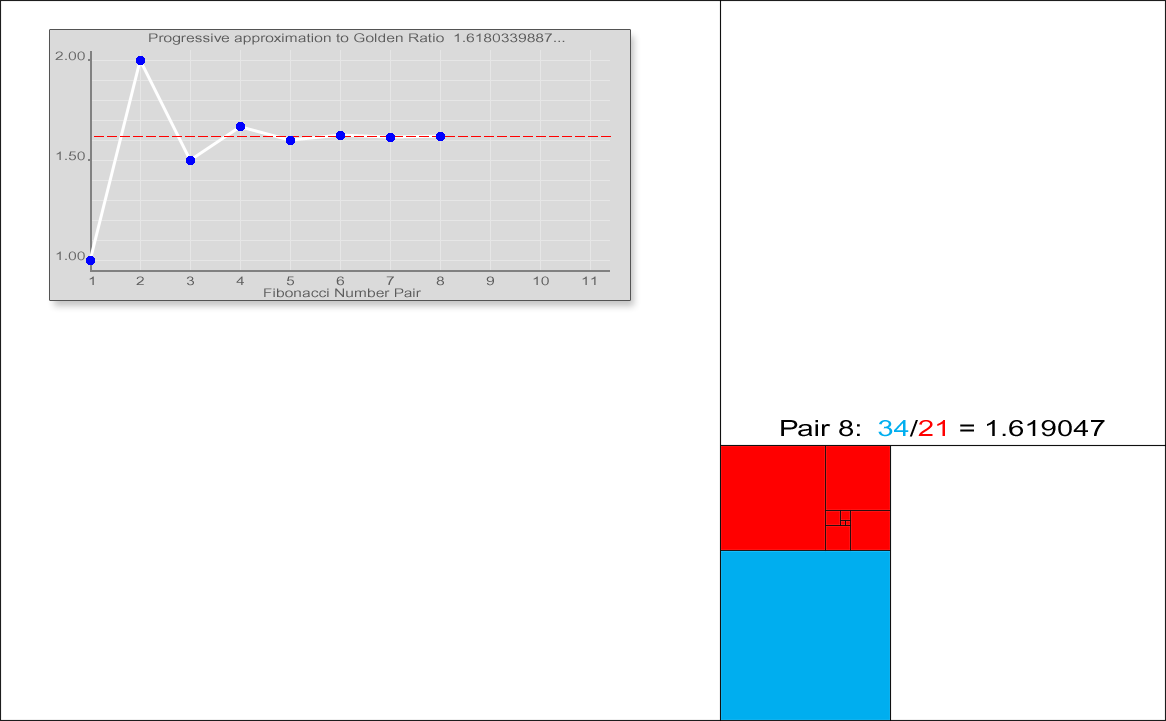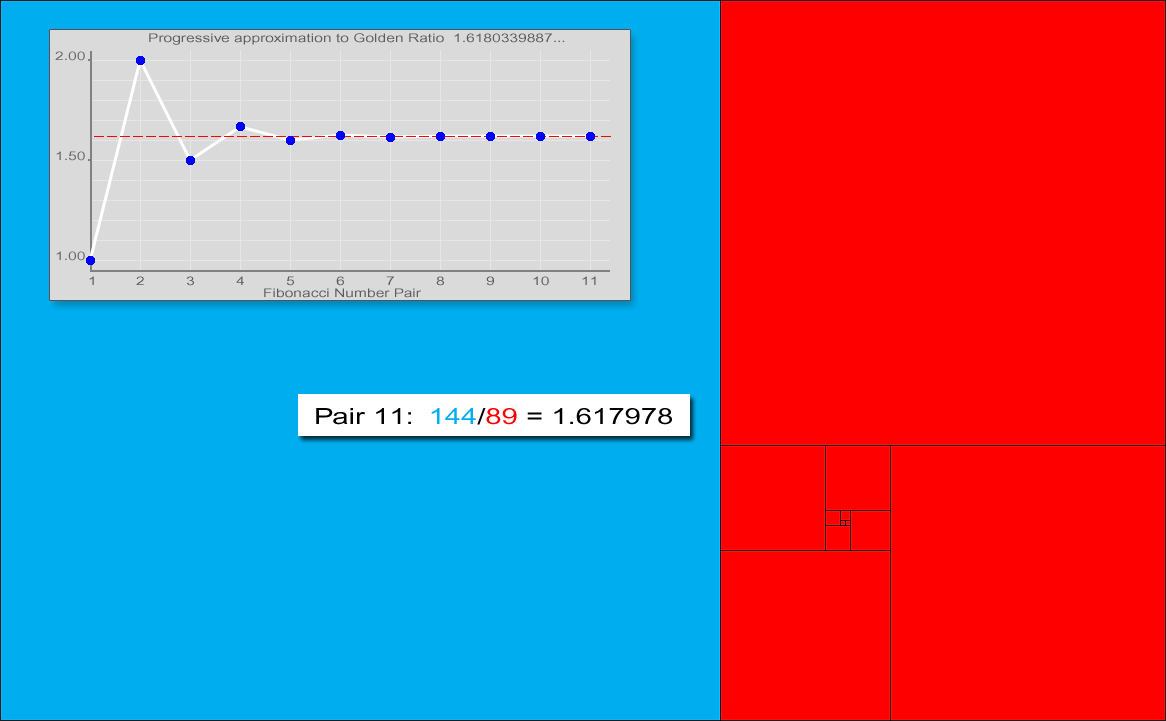
피보나치 수열에서 이웃하는 두 항의 비는
:
이 성질은 피보나치 수열의 정의
또한, 피보나치 수는 황금비를 이용하여 다음과 같은 부등식으로 그 크기를 어림할 수 있다.[20]
:
피보나치 수열의 일반항은 '''비네 공식'''으로 알려져 있으며, 황금비
:
이 공식은 1843년 자크 필리프 마리 비네가 발표했지만, 그보다 앞서 아브라함 드무아브르 (1730년)와 레온하르트 오일러 (1765년)에 의해 알려져 있었다.
:
여기서
피보나치 수열의 점화식은 행렬을 이용하여 다음과 같이 표현할 수 있다.[3]
:
이를 반복 적용하면 다음 관계를 얻는다.
:
이 행렬 표현의 행렬식을 계산하면
:
:
:
4. 1. 급수 공식
처음 몇 피보나치 수의 합,[20] 교대합,[20] 제곱합,[20] 세제곱합[20]은 다음과 같다.:
:
:
:
처음 몇 피보나치 수의 홀수째,[20] 짝수째,[20] 3의 배수째[20] 항의 합은 다음과 같다.
:
:
:
피보나치 수의 역수의 합은 수렴하며, 또한 다음 항등식들이 성립한다.[20]
:
&=3+\sum_{n=1}^\infty\frac{(-1)^n}{F_nF_{n+1}F_{n+2}}\\
&=\frac{41}{12}-\frac32\sum_{n=1}^\infty\frac1{F_nF_{n+1}F_{n+2}F_{n+3}F_{n+4}}\\
&=\frac{11749}{5280}-\frac{60}{11}\sum_{n=1}^\infty\frac{(-1)^n}{F_nF_{n+1}F_{n+2}F_{n+3}F_{n+4}F_{n+5}F_{n+6}}
\end{align}
홀수 위치에서 피보나치 수의 역수의 합은 다음 값을 갖는다:
:
여기서 λ*은 모듈러 람다 함수이고, K는 제 1 종 완전 타원 적분이다.
4. 2. 생성 함수
피보나치 수의 생성 함수는 다음과 같다.[20]:
피보나치 수의 역수의 생성 함수는 다음과 같이 나타낼 수 있다.[20]
:
&=\sum_{n=1}^\infty\frac{x^n\sqrt5}{\varphi^n}+\sum_{n=1}^\infty(-1)^n\frac{x^n}{F_n\varphi^{2n}}\\
&=\frac{x\sqrt 5}{\varphi-x}+\sum_{n=1}^\infty(-1)^n\frac{x^n}{F_n(F_{2n}\varphi+F_{2n-1})}\\
&=\frac{x\sqrt 5}{\varphi-x}-\frac{x\sqrt 5}{\varphi^3+x}
+\sum_{n=1}^\infty\frac{x^n}{F_n\varphi^{4n}}\\
&=\frac{x\sqrt 5}{\varphi-x}-\frac{x\sqrt 5}{\varphi^3+x}+\frac{x\sqrt 5}{\varphi^5-x}
+\sum_{n=1}^\infty(-1)^n\frac{x^n}{F_n\varphi^{6n}}
\end{align}
4. 3. 수론적 성질
피보나치 수열에서 서로 인접한 항은 서로소이다.또한, 자연수 ''p'', ''q''의 최대공약수를 ''r''이라고 하면, ''F''''p''와 ''F''''q''의 최대공약수는 ''F''''r''이다. 이 성질로부터 다음과 같은 사실들을 유도할 수 있다.
- ''m''이 ''n''으로 나누어 떨어지면, ''F''''m''은 ''F''''n''으로 나누어 떨어진다.
- ''F''''m''이 짝수가 되는 것은 ''m''이 3의 배수일 때와 동치이다.
- ''F''''m''이 5의 배수가 되는 것은 ''m''이 5의 배수일 때와 동치이다.
- ''p''가 2도 5도 아닌 소수일 때, ''m'' = ''p'' − (5/''p'')라고 하면 ''p''는 ''F''''m''을 나눈다. 여기서 ( / )는 르장드르 기호이다.
피보나치 수 중 특정 형태의 수에 대한 성질은 다음과 같다.
- 제곱수인 피보나치 수는 ''F''1 = ''F''2 = 1, ''F''12 = 144 뿐이다 (Cohn 1964)[4].
- 세제곱수인 피보나치 수는 ''F''1 = ''F''2 = 1, ''F''6 = 8 뿐이다 (London and Finkelstein 1969)[5].
- 거듭제곱수인 피보나치 수는 위의 제곱수와 세제곱수 외에는 존재하지 않는다 (Bugeaud, Mignotte, Siksek 2006)[6]. (OEIS A227875)
- 소수인 피보나치 수는 2, 3, 5, 13, 89, 233, 1597, 28657, … 등이 있으며 (OEIS A005478), 이들을 피보나치 소수라고 부른다.
- 삼각수인 피보나치 수는 1, 3, 21, 55 (OEIS A039595) 뿐이다. 이는 Vern Hoggatt에 의해 추측되었고, 나중에 Luo Ming에 의해 증명되었다[7].
- 하샤드 수인 피보나치 수는 1, 2, 3, 5, 8, 21, 144, 2584, … 등이 있다 (OEIS A117774).
- 피보나치 수는 완전수가 될 수 없다[8]. 더 나아가, 피보나치 수는 배적 완전수도 될 수 없으며[9], 두 피보나치 수의 비 또한 완전수가 될 수 없다[10].
임의의 양의 정수는 하나 이상의 연속하지 않은 서로 다른 피보나치 수의 합으로 유일하게 표현할 수 있는데, 이를 제켄도르프 정리라고 한다.
5. 여러 가지 예시
피보나치 수열의 점화식은 다음과 같이 행렬로 표현할 수 있다.[3]
:
1 & 1 \\
1 & 0
\end{bmatrix} \begin{bmatrix} F_{n} \\ F_{n-1} \end{bmatrix},\;\;\begin{bmatrix} F_{n} \\ F_{n-1} \end{bmatrix} = \begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix} \begin{bmatrix} F_{n-1} \\ F_{n-2} \end{bmatrix}
이를 반복하여 적용하면 다음과 같은 행렬 관계식을 얻는다.
:
\begin{bmatrix}
F_{n+1} & F_{n} \\
F_{n} & F_{n-1}
\end{bmatrix} &= \begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}\begin{bmatrix}
F_{n} & F_{n-1} \\
F_{n-1} & F_{n-2}
\end{bmatrix} \\
&= \cdots \\
&= \begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}^n\begin{bmatrix}
F_{1} & F_{0} \\
F_{0} & F_{-1}
\end{bmatrix} \\
&= \begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}^n\begin{bmatrix}
1 & 0 \\
0 & 1
\end{bmatrix}
\end{align}
여기서
:
\begin{align}
\begin{bmatrix}
F_{n+1} & F_{n} \\
F_{n} & F_{n-1}
\end{bmatrix} = \begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}^n
\end{align}
또한, 위 행렬 관계식에서
:
\begin{bmatrix}
F_{2n+1} & F_{2n} \\
F_{2n} & F_{2n-1}
\end{bmatrix} &= \begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}^{2n} = \left ( \begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}^n \right )^2 = \begin{bmatrix}
F_{n+1} & F_n \\
F_n & F_{n-1}
\end{bmatrix}^2 \\
&= \begin{bmatrix}
F_{n+1}^2 + F_n^2 & F_n(F_{n+1} + F_{n-1}) \\
F_n(F_{n+1} + F_{n-1}) & F_n^2 + F_{n-1}^2
\end{bmatrix}
\end{align}
따라서, 다음과 같은 항등식을 얻는다.
:
F_{2n+1} &= F_{n+1}^2 + F_n^2 \\
F_{2n} &= F_n(F_{n+1} + F_{n-1}) = F_n(F_n + 2F_{n-1}) \\
F_{2n-1} &= F_n^2 + F_{n-1}^2
\end{align}
피보나치 수열의 모 생성 함수는 다음과 같다.
:
또한, 행렬 표현을 기반으로 다음과 같은 점화식을 생각할 수도 있다.
:
F_0 = 0 & \, \\
F_1 = 1 & \, \\
F_n = F_q^2+\{ 1+(-1)^n \}F_{q-1}F_q+\dfrac{1-(-1)^n}{2}F_{q+1}^2 &\left( n\geqq 2,\;q=\left\lfloor \dfrac{n}{2} \right\rfloor \right)
\end{cases}
피보나치 수열은 재귀 처리의 예시로 자주 소개된다. 다음은 파이썬에서의 예시이다.
(단, 아래 구현 예시 중 음수 번째 항으로의 확장에 대응하는 것은 예시 5, 예시 6뿐이다.)
5. 1. 자연 속의 피보나치 수열
(원본 소스에 해당 섹션 내용이 존재하지 않아, 내용을 작성할 수 없습니다.)5. 2. 금융 분야
환율 등의 기술적 분석에서, 피보나치 되돌림이라는 기법이 자주 사용된다.6. 유사 수열
피보나치 수열은 그 정의, 즉 초기값이나 점화식을 약간 변경하여 다양한 유사 수열을 만들 수 있다. 예를 들어, 각 항이 바로 앞 두 항의 합으로 결정되는 규칙 대신, 더 많은 이전 항들의 합으로 새로운 항을 정의하는 방식으로 일반화할 수 있다. 또한, 수열의 시작 값인 처음 몇 개의 항을 다르게 설정하여 또 다른 종류의 유사 수열을 만들 수도 있다. 이러한 방식으로 생성된 수열들은 피보나치 수열과 유사한 성질을 가지면서도 독특한 특징을 나타낸다.
6. 1. 항 수 변경
피보나치 수열은 각 항이 바로 앞 두 항의 합으로 이루어지지만, 이를 "바로 앞 ''k'' 항의 합"으로 바꾸어 일반화할 수 있다.:
이러한 일반화된 피보나치 수열을 정의할 때는 초기값을 설정하는 방식이 필요하다. 주로 두 가지 방식이 사용된다.
- 1-fil형: 처음 ''k''-1개 항을 모두 1로 설정한다.
:
- 0-fil형: 마지막 항인 (''k''-1)번째 항만 1로 설정하고, 그 앞의 항들은 모두 0으로 설정한다.
:
이처럼 일반화된 피보나치 수열들은 항 수 ''k''에 해당하는 라틴어 또는 그리스어 배수 접두사와 '피보나치'를 조합하여 이름을 붙인다.[18] 예를 들어, ''k''=3일 때는 트리보나치 수열, ''k''=4일 때는 테트라나치 수열이라고 부른다.
| k | 접두사[18] | 명칭 | OEIS 링크 |
|---|---|---|---|
| 3 | tri- | 트리보나치 수 | 0 fil: OEIS: A000073 1 fil: OEIS: A000213 |
| 4 | tetra- | 테트라나치 수 | 0 fil: OEIS: A000078 1 fil: OEIS: A000288 |
| 5 | penta- | 펜타나치 수 | 0 fil: OEIS: A001591 1 fil: OEIS: A000322 |
| 6 | hexa- | 헥사나치 수 | 0 fil: OEIS: A001592 1 fil: OEIS: A000383 |
| 7 | hepta- | 헵타나치 수 | 0 fil: OEIS: A122189 1 fil: OEIS: A060455 |
| 8 | octa- | 옥타나치 수 | 0 fil: OEIS: A079262 1 fil: OEIS: A123526 |
| 9 | nona- | 노나(보)나치 수 | 1 fil: OEIS: A127193 |
| 10 | deca- | 데카(보)나치 수 | 1 fil: OEIS: A127194 |
| 11 | undeca- | 운데카(보)나치 수 | 1 fil: OEIS: A127624 |
| 12 | dodeca- | 도데카(보)나치 수 | 1 fil: OEIS: A207539 |
| ⋮ | ⋮ | ⋮ | ⋮ |
| 20 | icosa- | 이코사나치 수 | ⋮ |
특히 ''k''=3인 경우, 즉 바로 앞 세 항의 합으로 각 항이 정해지는 '''트리보나치 수열'''(Tribonacci sequence)은 피보나치 수열 다음으로 많이 연구된다. 0-fil형으로 0번째 항부터 시작하는 트리보나치 수열(
:
:
이 수열의 처음 몇 항은 다음과 같다.
:0, 0, 1, 1, 2, 4, 7, 13, 24, 44, 81, 149, 274, 504, 927, 1705, 3136, 5768, 10609, 19513, 35890, 66012, … (OEIS A000073)
트리보나치 수열의 일반항은 3차 방정식
:
여기서 세 해는 다음과 같다.
:
\alpha &= \frac{1}{3} \left(1 + \sqrt[3]{19-3\sqrt{33}} + \sqrt[3]{19+3\sqrt{33}}\right) \\
\beta &= \frac{1}{3} \left(1 + \omega \sqrt[3]{19-3\sqrt{33}} + \bar{\omega} \sqrt[3]{19+3\sqrt{33}}\right) \\
\gamma &= \frac{1}{3} \left(1 + \bar{\omega} \sqrt[3]{19-3\sqrt{33}} + \omega \sqrt[3]{19+3\sqrt{33}}\right)
\end{align}
(단,
이때 실수 해
:
''k''=4인 경우, 즉 바로 앞 네 항의 합으로 정해지는 '''테트라나치 수열'''(Tetranacci sequence)도 알려져 있다. 0-fil형으로 0번째 항부터 시작하는 테트라나치 수열(
:
:
이 수열의 처음 몇 항은 다음과 같다.
: 0, 0, 0, 1, 1, 2, 4, 8, 15, 29, 56, 108, 208, 401, 773, 1490, 2872, 5536, 10671, 20569, 39648, 76424, … (OEIS A000078)
테트라나치 수열의 일반항은 사차 방정식
:
6. 2. 초기값 변경
피보나치 수열의 처음 두 항을 2, 1로 바꾼 수열의 항을 뤼카 수라고 한다.: 2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521, 843, 1364, 2207, 3571, 5778, … (OEIS A000032)
이 수열의 일반항은
:
로 나타낸다.
피보나치 수열이나 뤼카 수의 열을 일반화한 것이 뤼카 수열이며, 1878년에 에두아르 뤼카가 체계적인 연구를 수행했고, 1913년에 Robert Daniel Carmichael|로버트 다니엘 카마이클eng이 그 결과를 정리, 확장했다[19]. 이러한 연구가 현대의 피보나치 수 이론의 기초가 되었다.
7. 프로그래밍 구현 (파이썬)
피보나치 수는 재귀 처리의 예시로 자주 소개된다. 다음은 파이썬을 이용한 다양한 구현 예시이다.
=== 재귀적 구현 ===
가장 기본적인 방법은 피보나치 수의 정의를 그대로 코드로 옮긴 재귀 함수를 사용하는 것이다. 0번째 항부터 시작하는 경우, 코드는 다음과 같다.
def fib(n):
if n == 0 or n == 1:
return n
return fib(n-2) + fib(n-1)
또는 타입 힌트를 사용하여 다음과 같이 작성할 수도 있다.
def fib(n: int) -> int:
if n < 2:
return n
else:
return fib(n=n-1) + fib(n=n-2)
그러나 이 방식은 ''n''이 주어졌을 때 ''Fn''을 구하기까지 ''Fn'' ∝ ''φn'' (여기서 ''φ''는 황금비) 번의 함수 호출이 발생하여 지수 시간 복잡도를 가진다. 즉, ''n''이 조금만 커져도 계산 시간이 매우 길어져 실용적이지 않다.
=== 메모이제이션을 이용한 재귀적 구현 ===
재귀적 구현의 비효율성을 개선하기 위해 메모이제이션 기법을 사용할 수 있다. 이미 계산된 피보나치 수 값을 저장해두고, 필요할 때 다시 계산하는 대신 저장된 값을 사용하는 방식이다.
memo = {}
def fib(n):
if n == 0 or n == 1:
return n
if n not in memo:
memo[n] = fib(n-2) + fib(n-1)
return memo[n]
파이썬의 `functools` 모듈에 있는 `cache` 데코레이터를 사용하면 더 간편하게 메모이제이션을 구현할 수 있다.
from functools import cache
@cache
def fib(n: int) -> int:
if n < 2:
return n
else:
return fib(n=n-1) + fib(n=n-2)
메모이제이션을 사용하면 각 피보나치 수는 한 번만 계산되므로 선형 시간 복잡도로 계산할 수 있다.
=== 반복적 구현 ===
반복문을 사용하여 피보나치 수를 계산할 수도 있다. 이 방법은 재귀 호출의 오버헤드가 없고 메모리 사용량도 적어 효율적이다.
def fib(n: int) -> int:
a, b = 1, 0 # F_1, F_0 에 해당하는 값으로 시작 (n=0일 때 b=0 반환)
for _ in range(n):
a, b = b, a+b # 다음 항 계산 (b가 F_k, a+b가 F_{k+1}이 됨)
return b # n번 반복 후 b는 F_n이 됨
이 구현 역시 선형 시간 복잡도를 가진다.
=== 꼬리 재귀 형태의 구현 ===
일부 언어에서는 꼬리 재귀 최적화를 지원하지만, 표준 파이썬 인터프리터는 이를 지원하지 않는다. 그러나 꼬리 재귀와 유사한 형태로 함수를 작성하여 반복적인 계산 과정을 표현할 수 있다. 이 방식은 추가적인 인자를 사용하여 상태를 전달한다.
def fib(n: int, a: int = 1, b: int = 0) -> int:
# a는 F_{k+1}, b는 F_k 에 해당하는 값을 가짐
if n == 0:
return b # n번 반복 후 b는 F_n
else:
# 다음 단계로 상태 업데이트 (a -> b, b -> a+b)
return fib(n=n-1, a=b, b=a+b)
이 함수는 ''n''이 1 이상일 때, 호출 횟수를 ''n'' 회로 제한하여 선형 시간으로 처리할 수 있다.
=== 행렬 표현을 이용한 구현 ===
피보나치 수열의 점화식은 다음과 같이 행렬로 표현할 수 있다.[3]
:
이를 반복 적용하면 다음 관계식을 얻는다.
:
여기서 ''n''을 ''n'' - 1로 치환하면,
:
따라서 ''Fn''은 행렬
from sympy import Matrix
def fib(n: int) -> int:
if n == 0: # 행렬 거듭제곱은 n-1을 사용하므로 n=0 예외 처리
return 0
# (n-1) 거듭제곱 계산 후 좌상단 성분 반환
return (Matrix(1, 1], [1, 0) ** (n - 1))[0, 0]
또한, 행렬 표현에서 유도된 다음 점화식을 사용하여 재귀적으로 구현할 수도 있다. 이 방식은 재귀 호출 횟수를 줄여 대수 시간(로그 시간) 복잡도를 가진다.
:
이를 코드로 구현하면 다음과 같다. 단, 프로그램 상에서는 0을 곱하는 경우에도 해당 값의 계산이 생략되지 않으므로(단락 평가되지 않음), 조건식을 사용하여 분기한다. 실제 효율적인 사용을 위해서는 메모이제이션이 필수적이다.
# 이 구현은 앞서 정의된 fib 함수에 의존하며, 메모이제이션과 함께 사용해야 효율적이다.
# 여기서는 설명을 위해 독립적인 함수 형태로 제시하며, 실제 사용 시에는 메모이제이션 적용 필요.
memo_fast = {}
def fib_fast(n: int) -> int:
if n in memo_fast:
return memo_fast[n]
if n < 2:
return n
q = n // 2
fq = fib_fast(n=q)
fq_minus_1 = fib_fast(n=q-1) # F_{q-1}
if n % 2 == 0: # n이 짝수일 때 F_n = F_q^2 + 2 * F_{q-1} * F_q
result = fq ** 2 + 2 * fq_minus_1 * fq
else: # n이 홀수일 때 F_n = F_q^2 + F_{q+1}^2
# F_{q+1} = F_q + F_{q-1} 이므로 다시 계산할 필요 없이 사용 가능
fq_plus_1 = fq + fq_minus_1
result = fq 2 + fq_plus_1 2
memo_fast[n] = result
return result
# 초기 호출 예시 (메모이제이션 딕셔너리 초기화 필요)
# memo_fast = {}
# print(fib_fast(10))
'''주의:''' 위 `fib_fast` 코드는 설명을 위한 것이며, 실제 효율적인 사용을 위해서는 `fib_fast` 함수 내에서 재귀 호출 시에도 `fib_fast`를 호출하고, 전역 또는 클래스 멤버 등으로 `memo_fast` 딕셔너리를 관리하여 메모이제이션을 올바르게 적용해야 한다.
=== 일반항을 이용한 구현 ===
비네 공식으로 알려진 피보나치 수의 일반항을 이용하여 계산할 수도 있다.
:
여기서
부동소수점 연산을 사용하면 계산 오차가 발생할 수 있으므로, 정확한 계산을 위해 파이썬의 `decimal` 모듈을 사용할 수 있다.
from decimal import Decimal, getcontext
# 필요에 따라 정밀도 설정 (예: getcontext().prec = 50)
SQRT5 = Decimal(5).sqrt()
PHI = (1 + SQRT5) / 2 # 황금비
def fib(n: int) -> int:
if n == 0: return 0
# |PSI^n / sqrt(5)|는 n이 커짐에 따라 0에 수렴하며, n >= 1에 대해 0.5보다 작다.
# 따라서 F_n은 PHI^n / sqrt(5) 에 가장 가까운 정수이다.
# F_n = round(PHI**n / SQRT5)
# PSI = -1/PHI 관계를 이용하여 계산할 수도 있다.
return int(round((PHI n - (-PHI) -n) / SQRT5))
또한, 피보나치 수의 일반항은 ''n''의 부호에 따라 두 항 중 하나의 절댓값이 0.5 미만이 되므로, 부호 함수와 바닥 함수를 사용하여 다음과 같이 나타낼 수도 있다.
: